Как устроено пространство событий теории физического вакуума

       Рассмотрим сначала пространство событий теории физического вакуума со структурой геометрии Вайценбека. Это пространство образует множество относительных координат произвольно ускоренных (с учетом вращения) систем отсчета, и его использование в физике приводит к объединению вращательной и общей относительности.

       Пространство имеет десять измерений, которые образуют четыре трансляционных координаты х, у, z, x0 = ct и шесть вращательных: ф1, ф2, ф3, q1, q2, q3. Почему десять координат? Ответ простой - произвольно ускоренная система отсчета, образованная четырьмя ортогональными векторами, имеет десять степеней свободы и, следовательно, должна описываться десятью координатами.

       Пространство событий теории физического вакуума не только искривлено и закручено. Что такое кривизна пространства? Представим себе половину длины окружности и проведем через концы этой кривой ось вращения. Заставим кривую вращаться (см. рис. 18). В результате кривая будет заметать двумерную поверхность, образующую сферу. Поверхность сферы представляет собой двумерное искривленное пространство. Если провести на поверхности сферы параллельные линии - меридианы, то они пересекутся на полюсах. Напомним, что в плоских геометриях, например, в геометрии Евклида, параллельные линии не пересекаются, сколько бы мы их не продолжали.

Рис. 18. Вращение половины длины окружности вокруг оси, проходящей через диаметр, заметает в пространстве двумерную сферу. Поверхность сферы представляет собой двумерное искривленное пространство.

Рис. 19. Перекрученная бумажная лента в пределе, когда ее ширина стремится к нулю, превращается в закрученную линию.

       А как можно представить закрученное пространство? Пусть мы имеем бумажную ленту (см. рис. 19). Закрепим один конец ленты, а другой будем поворачивать. В результате получим скрученную ленту. Устремим ширину ленты к нулю, тогда в пределе мы получим скрученную линию. Единичный вектор, присоединенный к какой-нибудь точке этой линии, будет вращаться по мере передвижения вектора вдоль линии. Если теперь взять закрученную полуокружность на рис.18 и начать вращать ее вокруг диаметра, то мы получим сферу, поверхность которой будет не только искривлена, но и закручена. Траектории частиц, принадлежащие такой поверхности, будут соответствовать движению в некотором силовом поле с учетом вращения вокруг собственной оси (т.е. с учетом «классического» спина). Это был пример двумерного по трансляционным координатам искривленного и закрученного пространства, в то время как пространство теории физического вакуума по трансляционным координатам четырехмерно.

       Если рассматривать одни лишь трансляционные координаты, то в специальной теории относительности, в теории Эйнштейна и общерелятивистской электродинамике доступное наблюдателю пространство событий находится внутри и на поверхности светового конуса будущего (см. рис 20).

       После создания модели электрон-позитронного вакуума, Дирак предложил рассматривать позитрон как электрон, который движется вспять по времени, т.е. в прошлое. Впоследствии все античастицы стали рассматривать как соответствующие им частицы, движущиеся вспять по времени. Поэтому в квантовой теории поля на микроуровне пространство событий включает в себя (дополнительно к конусу будущего) конус прошлого.

       В теории физического вакуума допустимыми оказываются все области пространства событий (см. рис. 20). Этот вывод следует из двух теоретических следствий новой теории.

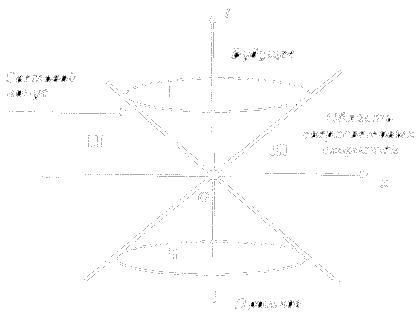
Рис. 20. Различные области пространства событий. I - пространство специальной и общей теории относительности, I + II - то же квантовой теории поля; I + II + III - теории физического вакуума.

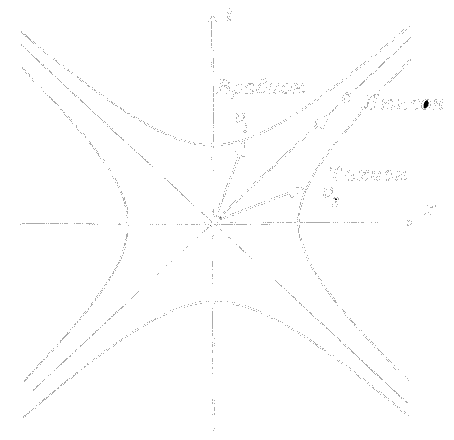
Рис. 21. Триплетный характер решений уравнений физического вакуума. Скорости решений. V1 - брадионного, с - люксонного; V2 - тахионного.

       Во-первых, решения уравнений вакуума носят триплетный характер. Каждое решение описывает один и тот же объект, но этот объект может проявить себя либо как брадион - частица, которая движется со скоростью меньше скорости света, либо как люксон - частица, которая движется со скоростью света, либо как тахион - частица, которая движется со сверхсветовыми скоростями (см. рис. 21).

       Из специальной теории относительности известно, что тахионы обладают мнимой энергией и, следовательно, мнимой массой: m = iЕc2. Известна так же теорема, согласно которой системы, состоящие из совокупности положительных и мнимых масс, могут иметь отрицательную массу.

       Во-вторых, закон сохранения энергии при рождении из вакуума положительных масс требует одновременного рождения масс отрицательных. Отрицательные массы порождают отрицательные энергии: Е = - mc2, a отрицательные энергии соответствуют частицам, которые движутся вспять по времени (внутри и на поверхности конуса прошлого).

       Рассмотрим теперь свойства пространства Вайценбека-Вейля, структурой которого обладает множество относительных координат конформных систем отсчета (см. рис. 14). Такое пространство имеет 15 координат. Пять дополнительных координат включают в себя:

       а) четыре специальных конформных координаты, описывающих композицию инверсии, трансляции и повторной инверсии;

       б) пятая координата соответствует конформным растяжениям.

       Замечательным свойством пространства Вайценбека-Вейля оказывается равноправие бесконечно удаленной точки со всеми остальными точками пространства. Отсюда следует важный для физики вывод - рождение каких-либо объектов из вакуума является существенно нелокальным процессом, поскольку в нем участвуют бесконечно удаленные точки пространства.